library(igraph)
set.seed(42)
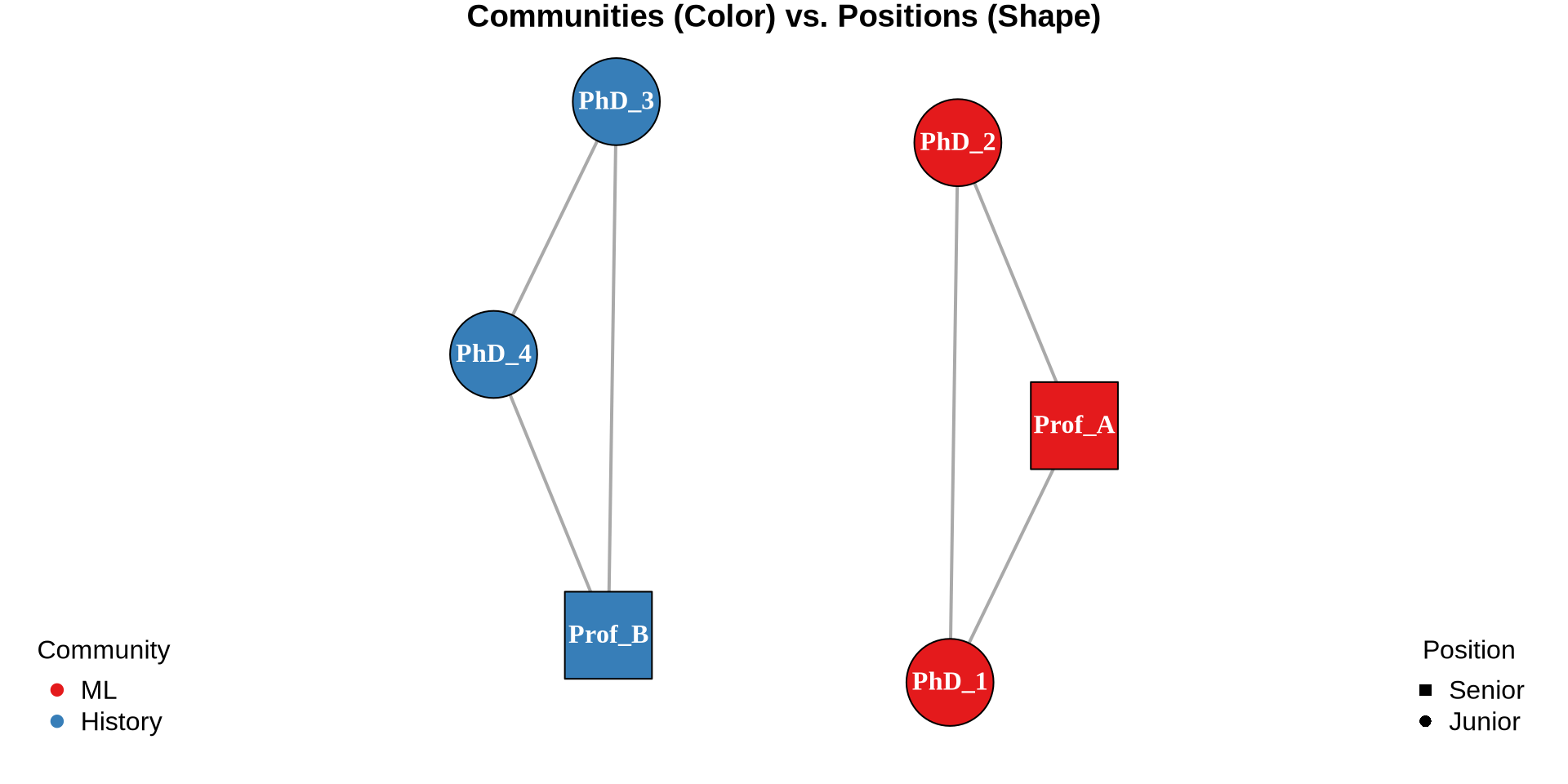
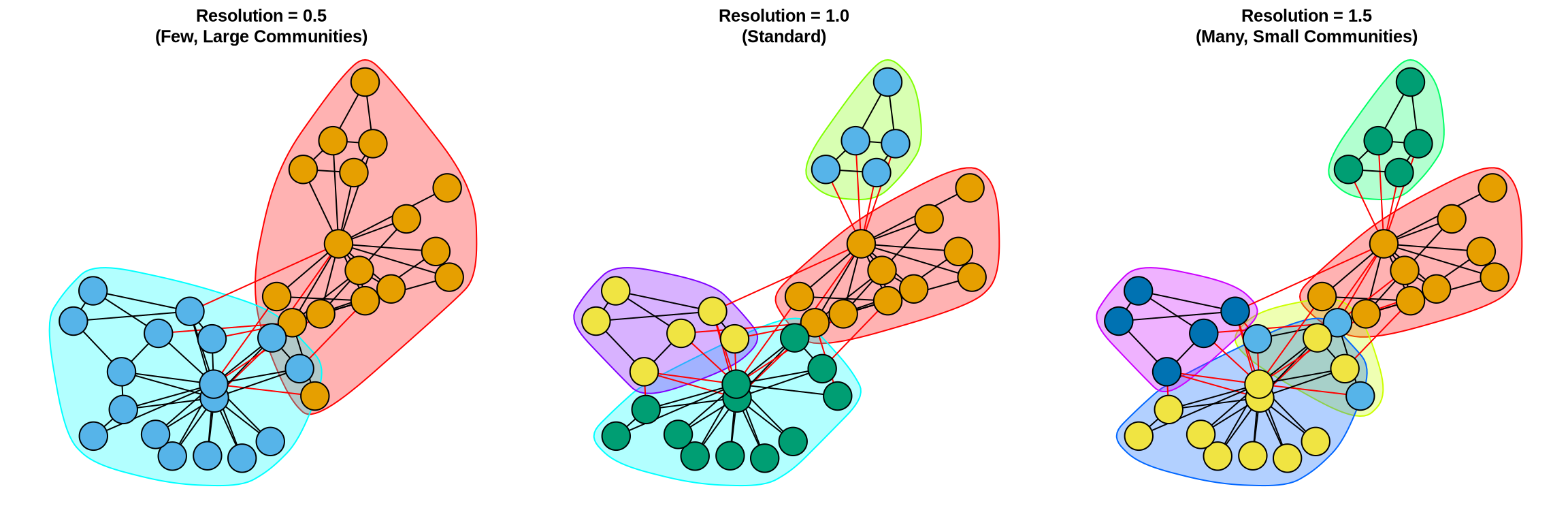
# Create a network with clear positional structure
# 3 "leaders" (high out-degree), 6 "followers" (high in-degree), 3 "isolates"
g <- make_empty_graph(n=12, directed=TRUE)
g <- add_edges(g, c(
1,4, 1,5, 1,6, 1,7, # Leader 1 → Followers
2,5, 2,6, 2,7, 2,8, # Leader 2 → Followers
3,6, 3,7, 3,8, 3,9, # Leader 3 → Followers
4,1, 5,2, 6,3 # Some followers → leaders (feedback)
))
adj <- as.matrix(as_adjacency_matrix(g))
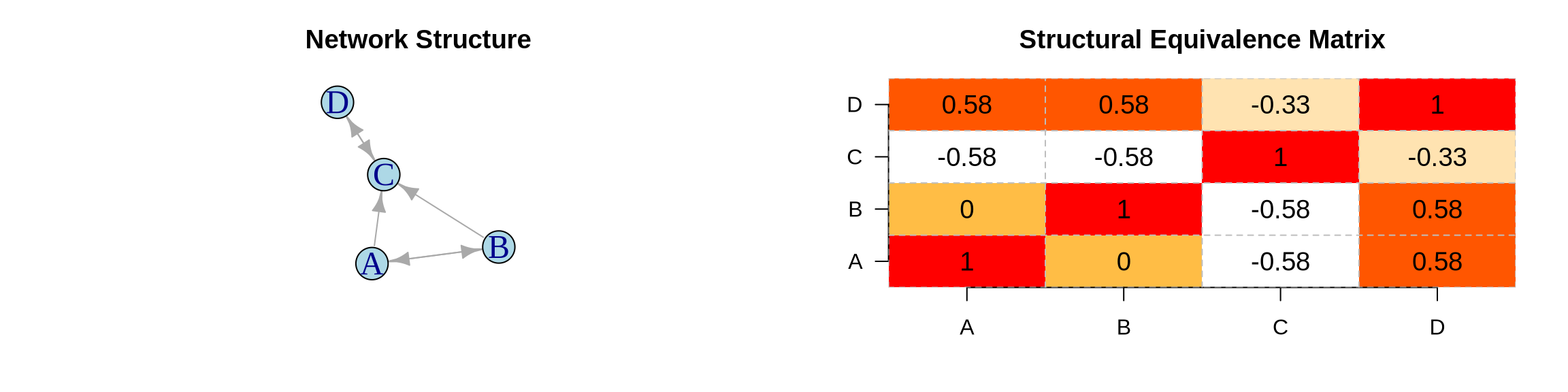
# Step 1: Compute Similarity Matrix (Correlation of tie patterns)
similarity <- cor(t(adj)) # Transpose to correlate rows
similarity[is.na(similarity)] <- 0 # Handle nodes with no ties
# Step 2: Hierarchical Clustering
dist_matrix <- as.dist(1 - similarity) # Convert similarity to distance
hc <- hclust(dist_matrix, method = "ward.D2")
positions <- cutree(hc, k = 3) # Cut into 3 positions
# Step 3: Create Blockmodel (Image Matrix)
n_pos <- max(positions)
blockmodel <- matrix(0, nrow = n_pos, ncol = n_pos)
for(i in 1:n_pos) {
for(j in 1:n_pos) {
block <- adj[positions == i, positions == j, drop=FALSE]
if(length(block) > 0) blockmodel[i, j] <- mean(block)
}
}
# Visualize the three outputs
par(mfrow=c(1,3), mar=c(4,4,3,2))
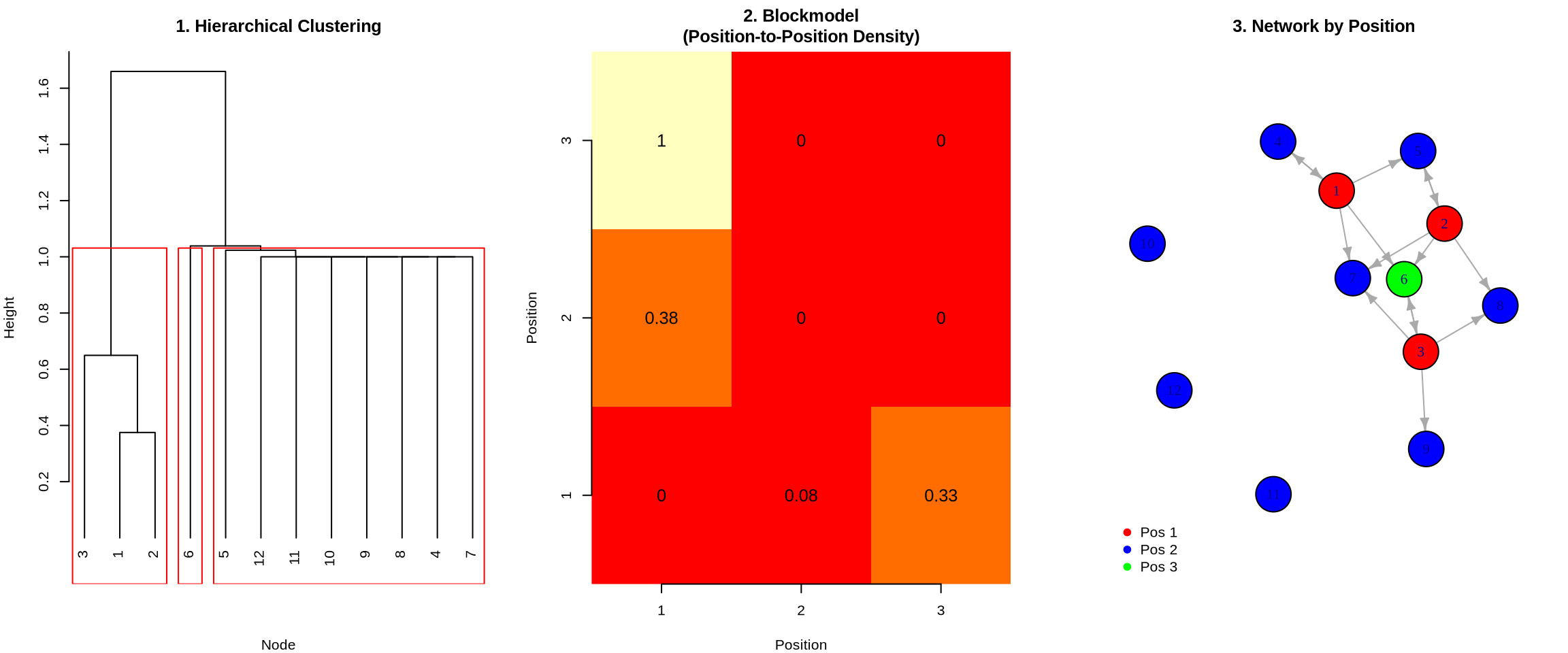
# 1. Dendrogram (Hierarchical Clustering)
plot(hc, main = "1. Hierarchical Clustering", xlab = "Node", sub = "", hang = -1)
rect.hclust(hc, k = 3, border = "red")
# 2. Image Matrix (Blockmodel)
image(1:n_pos, 1:n_pos, blockmodel, col = heat.colors(10),
main = "2. Blockmodel\n(Position-to-Position Density)",
xlab = "Position", ylab = "Position", axes = FALSE)
axis(1, at = 1:n_pos); axis(2, at = 1:n_pos)
text(expand.grid(1:n_pos, 1:n_pos), labels = round(blockmodel, 2), cex = 1.2)
# 3. Network colored by position
V(g)$color <- c("red", "blue", "green")[positions]
plot(g, vertex.size = 20, edge.arrow.size = 0.5,
main = "3. Network by Position",
vertex.label = 1:12)
legend("bottomleft", legend = paste("Pos", 1:3),
col = c("red", "blue", "green"), pch = 19, bty = "n")