SoundCloud Network Properties Analysis

Week 5 - Testing Reciprocity and Transitivity

Overview

This analysis examines two fundamental network properties in the SoundCloud follow network:

Reciprocity: The tendency for users to follow each other mutually (if A follows B, does B follow A?)
Transitivity (Clustering): The tendency for users to form triangles (if A follows B and B follows C, does A follow C?)

These properties help us understand the social structure and relationship patterns in the SoundCloud community.

Setup and Data Loading

# Load required libraries
library(tidyverse)
library(igraph)
library(knitr)
library(gridExtra)
library(sna)        # For CUG tests
library(network)    # For network objects (required by sna)
library(intergraph) # For converting between igraph and network objects

# Note: sna and igraph have some function name conflicts (e.g., degree, betweenness)
# When needed, we use igraph:: prefix to specify which package's function to use

# Set theme for plots
theme_set(theme_minimal())

# Configure output options
opts_chunk$set(
  echo = TRUE,
  message = FALSE,
  warning = FALSE,
  fig.width = 10,
  fig.height = 6
)

# Disable httpgd for compatibility
options(vsc.use_httpgd = FALSE)

# Set data path
data_path <- "../../../data/soundcloud/output/"

# Load follow network data
follows <- read_csv(paste0(data_path, "follows.csv"), show_col_types = FALSE)
users <- read_csv(paste0(data_path, "users.csv"), show_col_types = FALSE)

cat("Data loaded successfully!\n")

Data loaded successfully!

cat("Follow edges:", nrow(follows), "\n")

Follow edges: 60000

cat("Unique users:", n_distinct(c(follows$follower_id, follows$followee_id)), "\n")

Unique users: 8000

Network Construction

# Create directed graph from edge list
g <- graph_from_data_frame(
  d = follows[, c("follower_id", "followee_id")],
  directed = TRUE,
  vertices = NULL
)

# Network summary
cat("\n=== Network Summary ===\n")


=== Network Summary ===

cat("Nodes (users):", vcount(g), "\n")

Nodes (users): 8000

cat("Edges (follows):", ecount(g), "\n")

Edges (follows): 60000

cat("Density:", round(edge_density(g), 5), "\n")

Density: 0.00094

cat("Is directed:", is_directed(g), "\n")

Is directed: TRUE

cat("Is connected:", is_connected(g, mode = "weak"), "\n")

Is connected: TRUE

Reciprocity Analysis

Reciprocity measures the proportion of mutual connections in a directed network. A high reciprocity indicates that when user A follows user B, B is likely to follow A back.

Calculate Reciprocity

# Calculate reciprocity using different methods
recip_default <- reciprocity(g)
recip_ratio <- reciprocity(g, mode = "ratio")

cat("\n=== Reciprocity Measures ===\n\n")


=== Reciprocity Measures ===

cat("Reciprocity (default):", round(recip_default, 4), "\n")

Reciprocity (default): 0.0012

cat("  → Proportion of mutual edges among all edges\n\n")

  → Proportion of mutual edges among all edges

cat("Reciprocity (ratio):", round(recip_ratio, 4), "\n")

Reciprocity (ratio): 6e-04

cat("  → Proportion of reciprocated edges\n\n")

  → Proportion of reciprocated edges

# Calculate manually for verification
edges_df <- as_data_frame(g, what = "edges")
edges_df$edge_pair <- paste(
  pmin(edges_df$from, edges_df$to),
  pmax(edges_df$from, edges_df$to),
  sep = "_"
)

# Count mutual edges
mutual_pairs <- edges_df %>%
  count(edge_pair) %>%
  filter(n == 2) %>%
  nrow()

total_edges <- ecount(g)
manual_reciprocity <- (2 * mutual_pairs) / total_edges

cat("Manual calculation:", round(manual_reciprocity, 4), "\n")

Manual calculation: 0.0012

cat("  → Mutual pairs:", mutual_pairs, "\n")

  → Mutual pairs: 36

cat("  → Total edges:", total_edges, "\n")

  → Total edges: 60000

Reciprocity Interpretation

# Create interpretation dataframe
interpretation <- data.frame(
  Metric = c("Total Edges", "Mutual Pairs", "Reciprocity Rate", "Interpretation"),
  Value = c(
    format(total_edges, big.mark = ","),
    format(mutual_pairs, big.mark = ","),
    paste0(round(recip_default * 100, 2), "%"),
    ifelse(recip_default > 0.3, "High reciprocity",
           ifelse(recip_default > 0.1, "Moderate reciprocity", "Low reciprocity"))
  )
)

kable(interpretation, caption = "Reciprocity Summary")

Reciprocity Summary
Metric	Value
Total Edges	60,000
Mutual Pairs	36
Reciprocity Rate	0.12%
Interpretation	Low reciprocity

Visualize Reciprocal Relationships

# Classify edges as reciprocal or not
edge_types <- edges_df %>%
  group_by(edge_pair) %>%
  summarise(
    edge_count = n(),
    .groups = "drop"
  ) %>%
  mutate(
    type = ifelse(edge_count == 2, "Reciprocal", "One-way")
  )

# Count edge types
edge_type_summary <- edge_types %>%
  count(type) %>%
  mutate(
    percentage = round(n / sum(n) * 100, 1),
    edges_count = ifelse(type == "Reciprocal", n * 2, n)
  )

# Create visualization
ggplot(edge_type_summary, aes(x = type, y = edges_count, fill = type)) +
  geom_col(alpha = 0.8, width = 0.6) +
  geom_text(
    aes(label = paste0(format(edges_count, big.mark = ","), "\n(",
                       round(edges_count/total_edges*100, 1), "%)")),
    vjust = -0.5,
    size = 5
  ) +
  scale_fill_manual(values = c("Reciprocal" = "#50C878", "One-way" = "#c41c85")) +
  labs(
    title = "Distribution of Edge Types in Follow Network",
    x = "Edge Type",
    y = "Number of Edges",
    fill = "Type"
  ) +
  theme_minimal() +
  theme(legend.position = "none")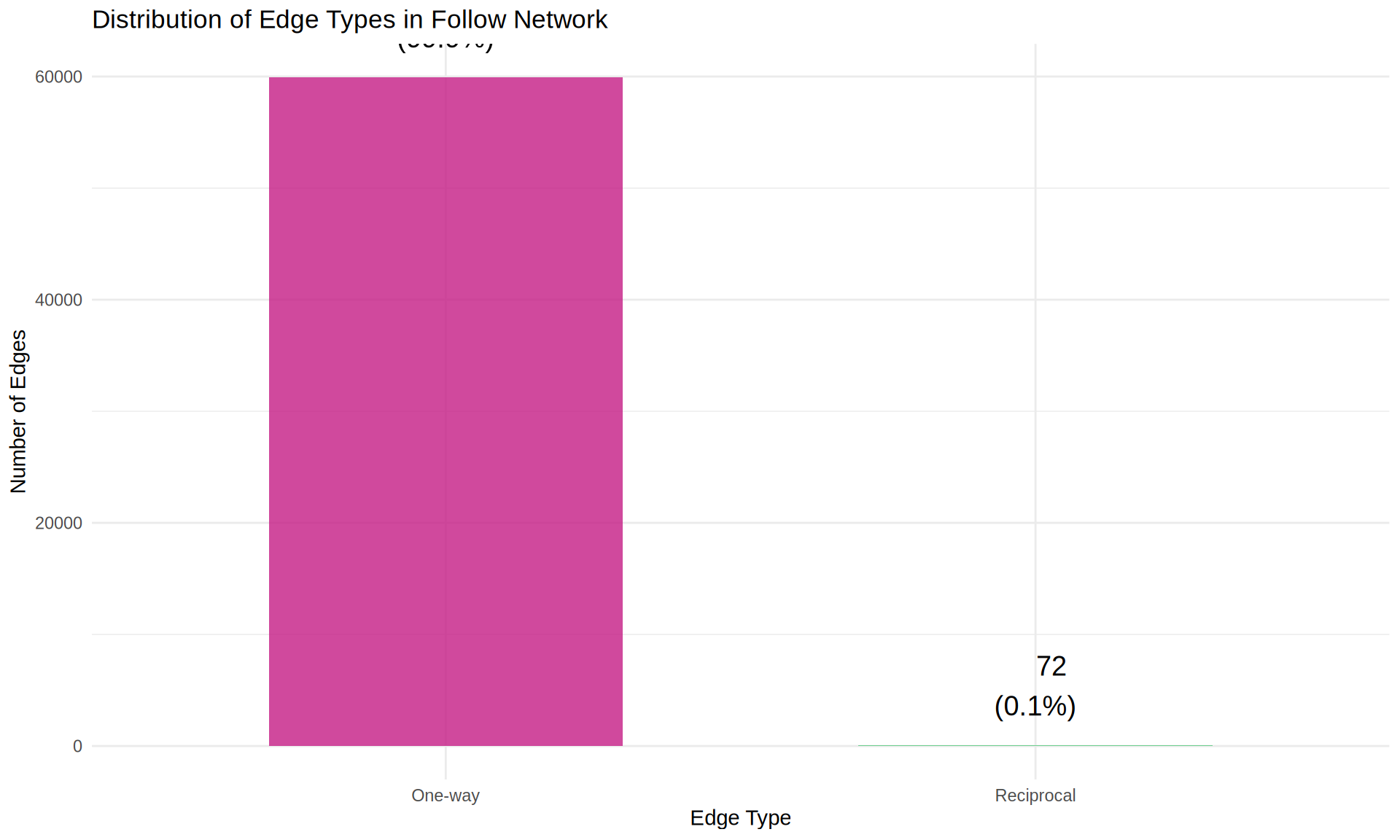

Distribution of reciprocal vs non-reciprocal edges

Transitivity Analysis

Transitivity (also called clustering coefficient) measures the probability that two neighbors of a node are also connected to each other. It quantifies the tendency to form triangles in the network.

Calculate Transitivity

# Global transitivity (clustering coefficient)
trans_global <- transitivity(g, type = "global")
trans_global_undirected <- transitivity(as.undirected(g, mode = "collapse"), type = "global")

# Average local transitivity
trans_local_avg <- transitivity(g, type = "average")

# Weighted transitivity (considers edge weights if present)
trans_weighted <- transitivity(g, type = "weighted")

cat("\n=== Transitivity Measures ===\n\n")


=== Transitivity Measures ===

cat("Global transitivity (directed):", round(trans_global, 4), "\n")

Global transitivity (directed): 0.0019

cat("  → Proportion of closed triplets (triangles) in the network\n\n")

  → Proportion of closed triplets (triangles) in the network

cat("Global transitivity (undirected):", round(trans_global_undirected, 4), "\n")

Global transitivity (undirected): 0.0019

cat("  → Ignoring edge direction\n\n")

  → Ignoring edge direction

cat("Average local transitivity:", round(trans_local_avg, 4), "\n")

Average local transitivity: 0.0019

cat("  → Average clustering coefficient across all nodes\n\n")

  → Average clustering coefficient across all nodes

cat("Weighted transitivity:", round(trans_weighted, 4), "\n")

Weighted transitivity: 0 0.0058 0 0 0 0.025 0 0 0 0 0 0.011 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0.0053 0 0 0 0 0 0.0131 0 0 0 0.0152 0 0.0278 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0.011 0 0.0128 0 0 0.0043 0 0 0 0 0 0.0065 0 0.0043 0 0 0.011 0 0 0 0.0053 0 0.0173 0 0 0 0 0 0.0222 0.011 0 0.0095 0 0 0 0 0 0 0 0.0152 0 0 0 0.0131 0.0065 0.0083 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0.011 0 0 0 0 0 0 0.0048 0 0 0 0 0 0 0 0 0.0095 0 0 0.0036 0 0 0 0 0 0 0 0.0065 0.0058 0 0 0 0.011 0 0 0.0083 0 0 0 0.0182 0.0053 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0.0065 0 0.004 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0.0058 0.0074 0 0.0048 0 0 0 0 0 0 0 0 0.0053 0.0058 0 0 0 0 0.0147 0 0 0.0128 0.0083 0.0222 0 0 0.0043 0 0 0.0048 0.0105 0.0083 0 0 0 0 0 0 0.0074 0.0058 0 0.0083 0 0 0.0105 0.0048 0 0 0 0 0 0 0.0053 0 0 0 0.0182 0.0131 0 0.0083 0 0 0.0222 0 0 0 0 0 0 0 0.0083 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0.0053 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0.0083 0 0 0 0.0128 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0.0053 0.0048 0 0.0058 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0.004 0 0.0058 0 0 0.0043 0.0095 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0.0053 0 0 0.0131 0 0 0 0 0 0 0.0065 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0.0065 0.0083 0.011 0 0 0 0.0083 0 0 0 0.0095 0 0 0 0 0.0083 0 0 0 0 0.0058 0 0.0128 0 0 0 0.0095 0 0.0083 0 0.0182 0 0 0 0 0 0 0 0.0058 0.0083 0 0 0 0 0 0 0 0 0 0.0095 0 0.0033 0.0058 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0.019 0 0 0.0053 0 0 0.004 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0.0095 0.0067 0 0 0 0 0 0 0 0 0 0 0.0095 0 0.0182 0 0.0074 0 0.0128 0 0.0048 0 0 0 0 0 0 0 0 0.0048 0.0043 0 0 0 0 0.0095 0 0 0 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0.0131 0 0.0074 0 0 0 0 0 0 0 0 0.0043 0 0 0 0 0 0 0 0.0065 0 0 0 0.0058 0 0 0 0 0 0 0 0.0303 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0.013 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0.0053 0.0083 0.0128 0 0 0 0 0 0 0.0083 0.0058 0 0 0 0 0 0 0.0048 0 0.0053 0 0 0 0 0 0 0.0053 0 0 0 0 0 0.0065 0 0 0 0 0.0053 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0.0065 0 0 0.0058 0 0 0 0 0.0095 0 0 0 0 0 0.011 0 0 0.0058 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0.004 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0.0128 0 0 0 0 0.0058 0 0 0 0 0 0 0 0.0083 0.0074 0 0 0.0152 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0.0364 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0.0062 0 0 0 0 0 0.0074 0 0 0 0.0065 0.0062 0 0 0.0117 0 0 0.0065 0 0.0074 0 0 0.0074 0 0 0 0 0.0303 0 0.0036 0.0083 0 0 0 0 0 0 0.0065 0.0058 0.0053 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0.0074 0.0095 0 0.0083 0 0 0.0065 0 0 0.0053 0 0 0 0 0 0.0053 0 0 0 0.0083 0.0053 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0057 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0.0067 0 0 0 0 0 0 0 0 0.0053 0.0065 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0.0048 0 0.011 0.0128 0 0 0 0.011 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0.0117 0 0 0 0.0058 0 0.0095 0 0.022 0 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0 0.0048 0 0 0 0 0 0 0 0.0128 0 0.004 0 0 0 0.004 0 0.0043 0.0131 0 0.0278 0 0 0 0.0095 0 0 0 0.0053 0 0.0095 0 0 0 0 0 0.0036 0 0 0.0043 0 0 0 0 0 0 0 0.0095 0 0 0 0 0 0.0053 0 0.0036 0 0 0 0 0 0 0.0095 0 0 0 0 0 0.0256 0 0 0 0.0167 0 0 0.0079 0.0048 0.0053 0 0 0 0 0 0 0 0.0053 0 0 0 0.0065 0 0 0.0087 0.0128 0 0 0 0 0 0 0 0.0053 0 0.0074 0 0 0 0 0.0105 0 0 0.0058 0.011 0.0105 0.011 0 0.0065 0 0 0.0083 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0182 0 0 0 0 0 0 0 0 0.0087 0.0058 0.0143 0.0065 0.019 0 0 0 0 0 0 0.0095 0 0 0 0 0.0083 0 0 0 0.011 0 0.0128 0 0.0065 0.0105 0 0 0.0074 0 0 0.0152 0 0 0 0 0 0.0065 0 0 0 0.0167 0 0.0074 0 0 0 0.0083 0 0 0.0128 0.0053 0 0 0 0 0 0 0 0 0 0 0.004 0 0 0.0065 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0.0033 0.0065 0.0053 0 0.0131 0 0 0 0 0 0.0048 0.011 0 0 0.0065 0 0 0 0.0083 0 0 0 0 0 0 0.0117 0 0 0 0 0 0 0.0043 0 0.011 0 0 0 0 0.011 0 0 0 0 0.0128 0.0053 0 0 0 0 0 0 0.011 0.0105 0 0 0.0065 0.0211 0 0 0 0 0 0 0 0 0 0 0 0.0058 0.0058 0.0444 0 0 0 0 0.011 0 0 0 0 0 0 0.0074 0 0 0.0128 0 0.0058 0.0131 0 0.0065 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0.0043 0 0 0 0 0 0.0083 0.0053 0.0074 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0.0117 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0 0 0 0.0095 0.0074 0 0 0.0278 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0.0074 0 0.0053 0.0083 0 0 0.0182 0.0058 0.0079 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0.0095 0 0 0.019 0 0 0 0 0 0 0.0095 0 0 0 0.0074 0 0 0.0095 0 0 0 0 0 0.0065 0.0048 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0.0083 0 0.0043 0 0 0 0 0.0053 0 0 0 0 0.0087 0 0 0 0 0 0.0065 0 0.0074 0 0 0 0 0 0.0083 0.011 0 0 0 0.0053 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0 0 0.0043 0 0 0 0 0 0.0033 0.0152 0 0 0.0043 0 0 0 0.0031 0 0 0 0 0 0 0 0 0 0.0128 0.0074 0.0048 0 0 0.0065 0 0 0 0 0.0117 0 0 0.0143 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0256 0.0043 0.0128 0 0 0.0031 0 0.0083 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0.0053 0 0 0 0 0 0.011 0 0 0 0.0053 0 0 0.0053 0 0 0 0 0 0 0 0 0 0.0074 0 0.0083 0.0095 0 0 0 0 0 0.0065 0 0.0058 0 0.0182 0 0 0 0 0.0058 0 0.0152 0 0.0152 0 0 0.011 0.0048 0 0.0095 0.0117 0 0.0128 0 0.0167 0 0 0 0.0072 0 0 0 0.0074 0.0128 0 0 0 0.0083 0 0 0.0083 0 0 0 0 0.0083 0 0 0.0092 0 0 0.0065 0 0 0 0 0 0 0 0 0 0.0131 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0048 0 0 0 0 0.0058 0 0 0 0 0.004 0 0 0.0095 0 0.011 0 0 0 0.0074 0 0 0.0053 0 0 0.0083 0 0 0 0 0.0065 0.0128 0 0 0.0058 0 0.011 0 0 0 0 0 0 0 0.0065 0 0 0.0053 0 0 0 0 0.022 0 0 0 0.0058 0.022 0 0.0128 0.0053 0 0 0 0 0.0128 0 0 0 0.0065 0 0.0048 0.0074 0 0 0.011 0 0 0 0 0 0.0065 0.0053 0 0 0 0 0 0 0 0 0 0.0222 0 0 0.0083 0 0 0 0 0.0083 0.0476 0 0 0 0 0.0048 0 0 0 0 0 0 0 0 0.0095 0 0.0058 0 0.0074 0 0 0 0.0095 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0.011 0.0048 0 0 0 0 0 0.0095 0 0 0.0058 0 0 0 0.0065 0 0.0074 0 0 0 0 0 0 0 0.0043 0 0 0 0 0 0 0 0.0053 0 0.0083 0 0 0 0 0 0 0 0 0 0.011 0.0128 0 0 0 0 0 0 0 0.0079 0 0 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0043 0 0 0.0095 0 0 0.0131 0 0.0095 0 0.0095 0 0 0 0.0053 0.0065 0.011 0 0 0 0.0033 0 0 0.0074 0 0 0 0 0.0058 0.0074 0.0095 0 0.0048 0 0 0 0 0 0 0 0 0 0 0 0.0128 0.0079 0 0 0 0.0182 0 0.0053 0 0 0 0 0 0 0 0.011 0 0 0 0.0131 0 0.025 0.0286 0 0 0 0.0128 0 0.0095 0 0 0 0 0 0 0 0 0.0043 0 0 0.0043 0 0 0 0 0 0 0.0057 0 0 0 0 0 0 0 0 0 0.0167 0 0 0 0 0 0 0.0095 0 0 0 0.0053 0.0083 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0.0043 0.0028 0 0.019 0 0.0074 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0.011 0 0 0.0058 0 0 0 0 0 0 0.0036 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0.0031 0 0 0 0.0074 0.0058 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0.0083 0 0 0.0058 0 0 0.0074 0.0053 0.0048 0.0095 0 0 0 0.0083 0 0.0095 0.0083 0 0 0 0 0.0074 0 0.0074 0 0 0 0 0 0 0.0222 0.0158 0 0 0.0053 0 0 0 0 0 0 0 0.0152 0 0.0048 0 0.0065 0 0 0 0 0 0.0053 0 0 0 0 0.0058 0 0 0 0 0 0.0058 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0.0256 0 0 0 0 0 0 0.0053 0 0 0.0053 0 0 0 0 0 0.0053 0 0 0 0 0 0.0083 0 0 0.011 0.0058 0.0036 0 0 0 0.0256 0.0074 0 0 0 0.0095 0 0 0 0 0 0.0074 0 0 0 0 0 0.0079 0 0.0031 0.0031 0 0 0 0 0.0079 0.0048 0 0 0.004 0 0 0 0.0074 0 0 0.0095 0 0 0 0.0278 0 0 0 0 0 0 0 0 0 0.0043 0 0 0 0 0 0 0 0 0.0058 0 0.0079 0 0 0.0074 0 0 0 0.0221 0.0152 0 0 0 0 0.0083 0 0 0.0028 0 0.0043 0 0 0 0.0053 0 0 0 0 0 0 0.0058 0 0 0.0074 0 0 0 0.0058 0.0048 0 0 0.0058 0 0 0 0 0 0.0152 0 0 0.0152 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0.004 0.0095 0.0074 0 0 0 0 0 0 0 0 0 0 0 0.0131 0 0 0 0 0 0 0 0 0.0256 0 0.0167 0.0128 0 0 0 0 0 0.0058 0 0 0 0 0.0105 0 0 0 0 0 0 0 0.0043 0 0.0083 0 0 0 0.0048 0 0 0 0 0.0095 0 0 0 0 0.011 0 0.0058 0 0 0 0.0053 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0.004 0 0.0074 0 0 0 0 0.0058 0 0 0 0 0 0 0.0065 0.0058 0 0 0 0 0 0 0.0053 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0 0 0.0286 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0.0065 0 0 0.0048 0 0 0 0 0 0 0 0.0036 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0.0053 0.0128 0 0 0.0053 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0147 0 0 0 0 0 0 0 0.0074 0.0095 0 0 0.0053 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0.0031 0 0 0 0.0072 0 0 0 0 0.0074 0.0147 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0.011 0 0 0.0053 0 0 0 0 0 0 0.0048 0 0 0 0 0 0 0.0152 0 0.0222 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0.0119 0 0.0065 0 0.0261 0 0 0 0 0 0.0065 0 0 0 0.0083 0 0 0 0 0 0 0 0.0117 0 0 0.0048 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0.0182 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0.0053 0 0 0.0067 0 0 0 0 0 0 0 0 0 0 0.0043 0 0 0.011 0 0 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0053 0.0083 0 0 0.0074 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0.0152 0 0 0.0053 0 0 0 0 0 0 0 0 0 0 0 0 0.0043 0 0.0095 0.0058 0 0 0 0 0 0 0 0 0.0053 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0.0147 0 0 0 0 0.0278 0 0.0074 0 0 0 0.0083 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0.0058 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0.0053 0 0 0 0 0.0117 0 0 0 0.0095 0 0.0065 0 0 0 0 0.0058 0 0 0 0.0058 0 0 0 0 0 0 0 0 0.0053 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0.0095 0 0 0.0095 0 0 0.0053 0 0 0.0095 0 0 0.0152 0 0 0 0 0 0 0 0 0.0065 0 0 0 0.0152 0.0058 0 0 0 0 0 0 0.0095 0.0074 0 0 0 0 0 0 0 0.0083 0.0058 0.0278 0 0 0 0 0 0 0.0303 0 0.0095 0.0152 0 0 0 0.0053 0 0.0105 0 0 0 0 0 0 0 0 0.0036 0 0 0 0 0 0 0 0 0 0 0.0065 0.011 0 0 0.011 0.0033 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0036 0 0.0128 0 0 0 0 0 0 0 0.0087 0 0.0152 0.0079 0 0.0182 0 0 0 0.0143 0 0 0 0.011 0.0074 0 0 0 0.0092 0 0.0083 0 0 0 0 0.0128 0 0.0058 0 0 0 0 0 0 0 0 0 0.011 0.0053 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0119 0 0 0 0.0065 0 0 0 0 0 0.0053 0 0 0 0.0036 0 0 0 0.0065 0.0053 0 0 0 0 0 0 0 0.011 0.011 0.0043 0 0 0 0 0 0 0 0 0.0182 0 0 0 0.0131 0.0048 0 0 0 0 0.0128 0 0.011 0 0.0128 0 0.0095 0 0 0 0 0 0 0.0065 0.0182 0 0 0 0 0 0.0065 0.011 0 0.0222 0 0 0 0.0074 0 0 0 0 0 0 0.004 0 0 0.0105 0.0128 0 0 0 0.0083 0 0.0128 0 0 0.0083 0 0 0.0083 0 0 0 0 0 0 0.0083 0 0 0 0 0.0058 0 0 0 0 0.0152 0 0 0 0 0 0 0.0053 0.0117 0 0.011 0 0 0 0 0 0 0 0 0 0.0128 0 0 0.0095 0 0 0 0 0 0 0 0 0.0083 0 0.0036 0 0.0053 0 0 0 0 0.0043 0 0 0 0 0 0 0.0147 0 0 0 0.019 0 0 0 0 0 0.0083 0 0 0 0 0.0058 0.0152 0 0 0 0 0 0 0 0 0 0.0095 0 0 0.0128 0.0048 0.0053 0.0048 0 0.0083 0 0 0 0.0053 0 0 0 0 0 0 0.0058 0 0 0 0 0.011 0.0043 0 0.0074 0 0 0 0 0 0 0.0058 0 0.0048 0.0065 0.0048 0 0 0 0 0 0 0.0074 0 0 0 0.0048 0 0 0 0 0.0058 0.0087 0 0.0074 0 0 0 0 0 0 0 0 0 0.0043 0.0095 0 0.011 0 0.0128 0 0 0 0 0.0065 0 0 0 0.0095 0 0 0 0.0182 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0105 0 0 0 0.0128 0.0065 0 0.0095 0 0 0 0 0 0 0 0 0.0065 0 0 0 0.0074 0 0 0 0.0074 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0.011 0 0 0 0 0 0 0 0.0074 0.0065 0.0074 0 0 0 0 0 0 0 0.0256 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0.0131 0 0 0 0 0.0048 0 0 0.0095 0 0 0 0 0.0074 0 0 0 0.0036 0 0 0 0 0 0 0.0058 0 0.0074 0 0 0.0048 0 0.0048 0 0 0.0065 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0.0053 0 0 0 0 0 0 0 0 0 0 0.0031 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0043 0 0 0 0.0152 0.0053 0 0 0.0058 0.0152 0 0 0 0 0 0.0087 0 0 0 0 0.0031 0 0.0083 0 0.0074 0.0167 0 0.0074 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0.0175 0 0 0 0 0 0.0058 0.0083 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0.0095 0.0147 0 0 0 0.0152 0 0.0065 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0058 0.0095 0 0.0074 0.0128 0.0065 0 0 0 0 0 0 0 0 0 0 0.0048 0.0083 0 0 0 0 0 0 0 0 0 0.011 0 0 0.0083 0 0 0.0222 0 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0 0 0.0095 0 0 0 0 0 0 0.0053 0 0 0 0 0 0 0 0.0182 0 0.0048 0 0 0 0 0 0 0.0083 0 0.0048 0 0 0 0 0 0 0 0 0 0 0 0.0117 0 0 0 0 0 0 0 0.0152 0 0 0 0 0.0053 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0.0175 0.0182 0 0 0 0 0 0 0 0 0 0 0 0.0198 0.004 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0.019 0 0 0 0 0 0 0 0.0095 0.0095 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0.0058 0 0.0043 0 0 0 0 0 0 0 0 0 0 0.0117 0.0083 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0 0 0 0 0 0.0048 0 0 0 0.0095 0 0.0074 0 0.0053 0.0048 0.0036 0.0083 0 0 0 0 0 0 0 0 0 0.0095 0 0 0.0053 0 0.0026 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0.0278 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0.0152 0 0 0.0058 0 0 0 0 0 0 0.0031 0 0 0 0 0 0 0 0 0 0.0117 0 0 0.0095 0 0.0128 0.0058 0.0048 0 0 0 0 0 0 0 0 0.0058 0.0043 0 0 0 0 0.0036 0.0074 0 0 0 0.0048 0.0053 0.0083 0.0095 0 0 0 0.0053 0.0048 0 0.0058 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0278 0.0357 0.022 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0.0158 0 0 0 0 0 0 0.0147 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0.0043 0 0.0043 0 0.0182 0 0 0 0 0 0 0 0 0 0.0065 0 0.0057 0.0083 0 0 0 0 0 0 0.0053 0 0 0.0083 0 0.0147 0 0 0 0 0 0 0 0.0067 0 0 0 0 0.0083 0.0083 0 0 0 0 0 0 0.011 0.0053 0.0053 0.0128 0 0 0 0 0 0.0043 0 0 0 0.0074 0 0.0043 0.0152 0 0 0 0 0 0 0 0.0182 0 0 0 0.0128 0 0 0 0.0105 0 0.0079 0 0.0095 0 0 0.0222 0 0 0 0.013 0.011 0 0 0.0256 0 0 0 0 0.0128 0.0095 0 0 0 0 0 0.0167 0 0 0 0.0095 0 0 0 0 0.0065 0 0.0058 0.0058 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0048 0.0182 0 0 0 0.0095 0 0 0 0.0043 0 0 0.0476 0 0.0083 0 0 0 0 0 0 0 0.0065 0 0 0.0083 0.0053 0 0.0095 0 0 0 0.0095 0 0 0 0.004 0.0053 0 0 0 0 0 0 0.0095 0 0 0 0.0033 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.004 0 0 0.0128 0 0 0.0058 0 0 0 0 0 0 0 0 0 0.0095 0 0.0128 0 0 0.0128 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0.0152 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0.0182 0.0182 0.0152 0 0 0 0.0083 0 0 0 0 0 0 0 0 0.0043 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0.011 0 0.0095 0.0058 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0117 0 0 0 0 0 0 0 0 0.0074 0.0036 0 0 0 0 0 0 0 0 0 0 0 0.0095 0.0095 0 0.0065 0 0 0.0065 0 0 0 0 0 0 0 0.0182 0 0.0074 0 0 0 0 0 0 0 0 0.0053 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0079 0.0152 0 0 0.011 0 0 0 0.0128 0 0 0.0128 0 0.0117 0 0.0095 0 0.011 0 0.011 0 0.0083 0 0 0 0 0 0.0182 0 0 0 0 0 0 0 0 0 0.019 0 0 0 0 0 0.011 0.0058 0.0053 0.0053 0 0 0 0 0 0 0 0.0087 0 0 0 0 0 0 0 0 0.0095 0 0 0.0256 0.0048 0.0062 0 0 0 0 0 0 0.0074 0 0.0182 0 0 0 0 0 0 0 0 0 0 0.0182 0 0 0 0.0128 0.0117 0 0 0 0 0 0 0 0.0043 0 0.0058 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0.0048 0.0043 0 0 0 0.011 0.011 0 0 0 0 0 0 0.004 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0.0128 0 0 0.011 0 0 0 0.0222 0 0 0 0 0.0053 0 0 0 0 0 0 0 0.0167 0 0.0074 0 0 0 0.0105 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.004 0 0 0 0 0 0.0182 0.0095 0 0 0 0 0.0065 0.0065 0 0 0 0 0 0.004 0 0 0 0 0 0 0 0 0.0074 0.0182 0 0 0.0036 0 0.0065 0.0048 0 0 0 0 0 0.0222 0 0 0 0 0 0.0043 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0 0 0.0083 0 0.0095 0 0 0 0.025 0 0 0 0.0128 0 0 0 0.004 0 0.0053 0 0 0 0 0.0128 0 0 0 0 0 0 0 0.0095 0 0 0 0 0.0065 0 0 0.0074 0 0 0 0 0 0 0 0.0043 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0147 0 0.0033 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0.0074 0 0.0182 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0.011 0.0074 0.0065 0 0 0 0 0.0152 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0.0095 0.0074 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0.0083 0 0.011 0.0053 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0.0095 0.0105 0.0048 0.0095 0 0.0058 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0278 0 0.0033 0.0048 0 0 0 0.0152 0 0 0 0 0 0 0 0 0.0065 0 0 0 0.0031 0 0.0182 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0.0095 0.0033 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0.0048 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0.011 0 0.0167 0 0 0 0 0 0.0131 0.0043 0.0048 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0.0074 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0256 0 0.0278 0.0043 0 0.0083 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0 0.022 0 0 0 0 0.0065 0 0 0 0 0.0182 0 0 0.019 0 0 0 0 0 0 0 0 0 0 0 0 0.0182 0 0 0 0.0105 0 0 0 0 0 0 0.0074 0 0 0 0.0167 0 0 0 0 0 0 0 0 0 0 0 0.0043 0 0 0.0182 0.011 0.0074 0 0 0 0 0 0.0128 0 0 0.0079 0 0 0 0 0 0 0 0 0 0 0 0.0036 0 0 0 0 0.011 0.0074 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0.0065 0 0 0 0.0087 0 0 0 0 0 0 0 0 0.0095 0 0 0.0119 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0182 0 0 0 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0.0128 0 0 0 0 0.0043 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0 0 0 0.0147 0 0 0 0 0 0 0.0065 0 0 0 0 0 0 0.0074 0.0058 0 0 0.0152 0.0095 0 0 0 0 0.0357 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0.011 0 0 0 0 0 0.011 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0.0357 0 0 0.0074 0 0 0 0.0065 0 0 0 0 0 0 0 0.0053 0 0 0 0 0 0 0 0.0058 0 0 0 0 0.0128 0 0 0 0 0.0222 0 0 0 0.0095 0 0 0.0048 0 0.0036 0 0 0.011 0 0 0 0 0 0 0 0.0065 0 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0.0053 0.0083 0 0 0.0036 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0.0476 0.0065 0.0117 0 0 0 0 0 0.0058 0 0 0 0 0 0 0 0 0.0074 0 0.0087 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0.011 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0147 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0.0131 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0.0033 0 0 0.022 0 0.0095 0 0 0 0 0 0 0 0.0053 0 0.019 0.0074 0 0.0065 0.0095 0 0 0 0 0 0 0 0 0 0.004 0.004 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0.0083 0 0.0083 0 0.0072 0.011 0 0 0 0.0147 0 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0.0083 0 0 0.0083 0 0 0 0.0074 0 0.004 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0065 0 0 0.0065 0 0 0 0 0 0 0 0 0.0095 0.0043 0 0 0 0 0.0058 0 0.0058 0 0 0 0 0 0.0152 0 0.0222 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0.0048 0 0 0 0 0.0065 0 0 0.0095 0 0 0 0 0 0 0 0 0.0074 0 0.0058 0 0 0 0 0 0 0.0095 0 0 0 0.0182 0.0182 0.0065 0 0 0 0 0 0 0 0.0182 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0.0083 0 0.0222 0 0 0 0 0.0095 0 0.0095 0 0 0 0 0.0095 0 0 0 0.011 0 0.0095 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0.0095 0.0074 0 0 0 0 0 0.0048 0 0.0053 0 0 0 0 0 0 0 0.019 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0.0083 0 0 0 0 0 0 0.0105 0 0 0 0.0083 0 0.0065 0 0 0 0 0.011 0 0 0 0.0058 0 0.0128 0 0.0083 0 0 0.0083 0 0 0 0.0058 0 0.011 0 0 0 0 0.0033 0 0 0 0 0 0 0 0 0 0 0 0.0048 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0.0095 0 0 0.011 0.0074 0.0046 0.0167 0 0 0 0.0128 0 0 0 0 0 0.0074 0.0095 0 0.022 0 0 0.0074 0 0 0 0 0 0.0152 0 0 0.0222 0.0074 0 0.0152 0 0.0095 0.022 0.019 0 0 0 0 0 0 0 0.004 0 0 0 0 0 0 0 0.0278 0 0 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0.0147 0 0 0 0 0 0 0 0 0 0 0 0.0105 0.0058 0 0.0095 0 0 0 0.011 0 0 0 0 0 0.0182 0.0074 0.0222 0.0128 0 0 0.0053 0 0.0043 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0.0128 0 0 0 0.0152 0.0087 0 0 0.0074 0 0.0057 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0222 0 0 0 0.0058 0 0 0 0 0.0143 0 0 0 0 0 0 0 0 0.0048 0 0.0128 0.0083 0 0 0 0 0.0058 0.0053 0 0 0 0 0.011 0 0 0.0074 0 0.011 0.0083 0 0 0 0.0128 0 0 0.0065 0 0 0.0074 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0.0128 0 0 0 0 0 0 0.0182 0.011 0 0 0 0.0065 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0.0095 0 0 0 0 0 0.0053 0.0058 0 0 0.0152 0 0.0095 0 0 0 0 0 0 0 0 0 0.022 0.0058 0 0 0.0095 0.0152 0.0053 0.0083 0 0.011 0.0065 0 0 0.0152 0 0 0 0 0 0.0053 0 0 0 0.0053 0 0 0 0 0 0 0 0 0 0 0.011 0 0.0074 0 0 0 0 0 0 0 0.0182 0 0 0 0 0.0182 0 0.0128 0 0 0 0 0.0167 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0 0.0095 0.0152 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0.0087 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0286 0.0182 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0.0256 0 0 0 0 0 0 0 0 0 0 0.0036 0 0 0 0.0167 0 0 0 0 0 0 0 0 0 0.022 0 0 0 0 0 0.0087 0 0 0 0.0095 0 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0 0.0074 0 0 0 0 0 0 0 0 0 0 0 0.0083 0.0074 0 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0.0074 0.011 0 0 0.0095 0 0.0278 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0.0058 0 0 0.0048 0.0128 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0083 0.011 0.0058 0 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0 0.0357 0 0 0 0 0 0 0 0 0 0 0.0167 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0.0182 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0.0083 0 0.0152 0.0053 0 0.0095 0.0095 0.0065 0 0.0095 0 0 0.0278 0 0 0 0 0 0 0 0 0.0048 0 0 0.0083 0.0128 0 0 0.0128 0 0 0.0152 0 0 0.0065 0 0 0 0 0.0222 0 0 0 0 0 0.0065 0 0.011 0 0 0 0 0 0 0 0 0 0.0182 0 0.0128 0 0.0278 0.019 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0182 0 0 0.0083 0 0 0 0.0222 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0.0065 0 0 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0.022 0 0 0 0 0 0 0 0 0 0 0 0 0.0053 0 0 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0.0053 0 0.0152 0 0 0 0 0 0 0 0 0.011 0 0 0 0.0083 0 0 0.0095 0 0 0.0083 0 0 0 0.0058 0 0 0.0182 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0 0 0 0.0083 0 0 0.0048 0.0182 0 0 0 0.0095 0 0 0 0.0058 0 0 0.0128 0.0303 0 0 0 0 0.0058 0.0058 0 0 0 0.0095 0 0 0 0 0 0.0083 0 0 0 0 0 0 0.0667 0.0074 0.0095 0 0 0 0 0.011 0 0 0 0 0 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0.0182 0 0 0 0 0.0222 0 0.0065 0 0.0043 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0.0167 0 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0.0095 0 0 0 0.0128 0.0053 0 0.0095 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0 0.011 0 0 0.0278 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0095 0 0 0 0.011 0 0 0 0 0 0 0 0.0095 0 0.0074 0 0 0 0 0.0083 0.0083 0 0 0.0278 0 0.0058 0 0 0 0 0 0 0.0065 0 0 0 0 0.0058 0 0 0 0 0 0.0087 0 0 0 0 0 0 0 0 0 0.0065 0.0278 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0117 0 0.0278 0.0182 0 0 0 0 0.0083 0 0 0.0095 0 0 0 0 0 0 0 0 0 0.0074 0 0 0 0.0667 0 0.0222 0 0 0 0 0 0 0 0 0.0303 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0.0095 0 0.0128 0 0 0 0 0 0 0 0 0.0182 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0.0222 0 0 0.0036 0 0.0058 0 0 0 0 0.0444 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0.0278 0 0 0 0.0065 0 0.0278 0 0.0053 0 0 0 0 0 0 0 0.0152 0 0 0 0.0065 0 0 0.0278 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0 0 0.0083 0 0 0.0128 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0182 0.0087 0 0 0 0 0 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.011 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0.0182 0 0 0 0 0 0 0 0 0 0 0.0147 0.0128 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0058 0.0357 0 0 0 0 0 0 0.0152 0 0 0 0.0074 0 0 0 0 0 0 0.0147 0 0 0 0 0 0 0 0 0 0.0065 0.0083 0 0 0 0 0 0.0128 0.0152 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0.0278 0 0.0152 0 0 0 0 0 0.0278 0 0 0 0 0.0083 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0476 0 0 0 0 0 0.0222 0 0 0 0 0 0 0 0 0 0 0.0357 0 0 0 0.0128 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0152 0 0 0 0 0 0 0.0128 0 0

cat("  → Accounts for node degrees\n\n")

  → Accounts for node degrees

Triangle Count Analysis

# Count triangles in the network
triangles_count <- sum(count_triangles(as.undirected(g, mode = "collapse"))) / 3
triad_census_result <- triad_census(g)

cat("\n=== Triangle Analysis ===\n\n")


=== Triangle Analysis ===

cat("Number of triangles (undirected):", triangles_count, "\n\n")

Number of triangles (undirected): 578

# Triad census for directed network (16 possible triad types)
cat("Triad Census (Directed Network):\n")

Triad Census (Directed Network):

cat("This shows counts of all 16 possible triad configurations\n\n")

This shows counts of all 16 possible triad configurations

# Create readable triad census
triad_names <- c(
  "003", "012", "102", "021D", "021U", "021C", "111D", "111U",
  "030T", "030C", "201", "120D", "120U", "120C", "210", "300"
)

triad_df <- data.frame(
  Type = triad_names,
  Count = as.vector(triad_census_result),
  Description = c(
    "Empty (no edges)",
    "Single edge",
    "Two edges (one mutual)",
    "Two edges (down)",
    "Two edges (up)",
    "Two edges (cycle)",
    "Three edges (down)",
    "Three edges (up)",
    "Three edges (transitive)",
    "Three edges (cycle)",
    "Four edges (one mutual)",
    "Four edges (down)",
    "Four edges (up)",
    "Four edges (cycle)",
    "Five edges",
    "Six edges (complete)"
  )
) %>%
  arrange(desc(Count)) %>%
  head(10)

kable(triad_df, caption = "Top 10 Triad Types", format.args = list(big.mark = ","))

Top 10 Triad Types
Type	Count	Description
003	84,822,641,507	Empty (no edges)
012	477,510,653	Single edge
021C	447,567	Two edges (cycle)
102	286,839	Two edges (one mutual)
021U	224,739	Two edges (up)
021D	223,028	Two edges (down)
111U	562	Three edges (up)
111D	527	Three edges (down)
030T	433	Three edges (transitive)
030C	145	Three edges (cycle)

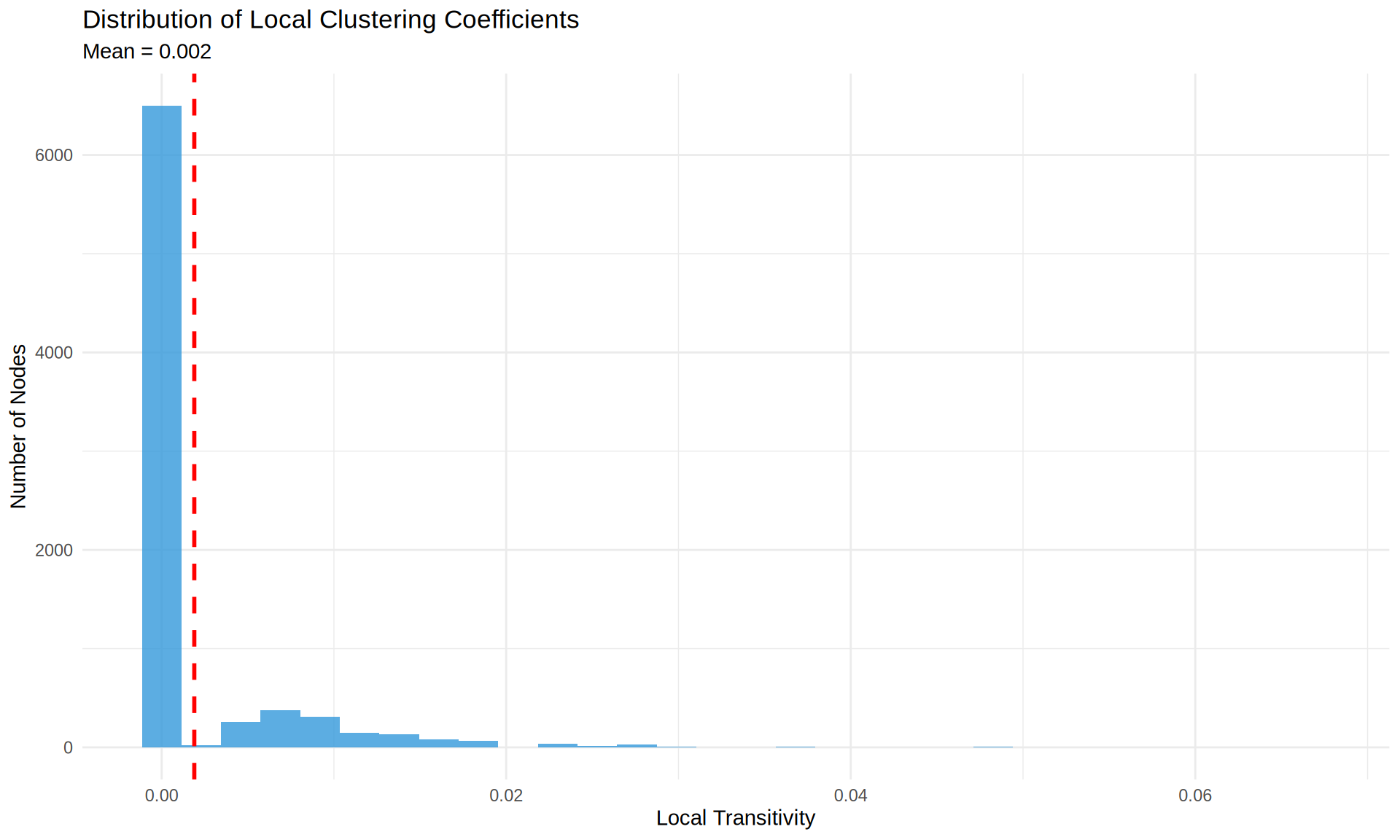
Local Transitivity Distribution

# Calculate local transitivity for each node
local_trans <- transitivity(g, type = "local", isolates = "zero")
local_trans[is.nan(local_trans)] <- 0

# Create dataframe with node properties
node_props <- data.frame(
  node = V(g)$name,
  local_transitivity = local_trans,
  degree = igraph::degree(g, mode = "all"),
  in_degree = igraph::degree(g, mode = "in"),
  out_degree = igraph::degree(g, mode = "out")
)

# Summary statistics
cat("\n=== Local Transitivity Statistics ===\n")


=== Local Transitivity Statistics ===

cat("Mean:", round(mean(local_trans, na.rm = TRUE), 4), "\n")

Mean: 0.0019

cat("Median:", round(median(local_trans, na.rm = TRUE), 4), "\n")

Median: 0

cat("SD:", round(sd(local_trans, na.rm = TRUE), 4), "\n")

SD: 0.0048

cat("Min:", round(min(local_trans, na.rm = TRUE), 4), "\n")

Min: 0

cat("Max:", round(max(local_trans, na.rm = TRUE), 4), "\n\n")

Max: 0.0667

# Visualize distribution
ggplot(node_props, aes(x = local_transitivity)) +
  geom_histogram(fill = "#3498db", bins = 30, alpha = 0.8) +
  geom_vline(
    xintercept = mean(local_trans, na.rm = TRUE),
    color = "red",
    linetype = "dashed",
    size = 1
  ) +
  labs(
    title = "Distribution of Local Clustering Coefficients",
    subtitle = paste0("Mean = ", round(mean(local_trans, na.rm = TRUE), 3)),
    x = "Local Transitivity",
    y = "Number of Nodes"
  )

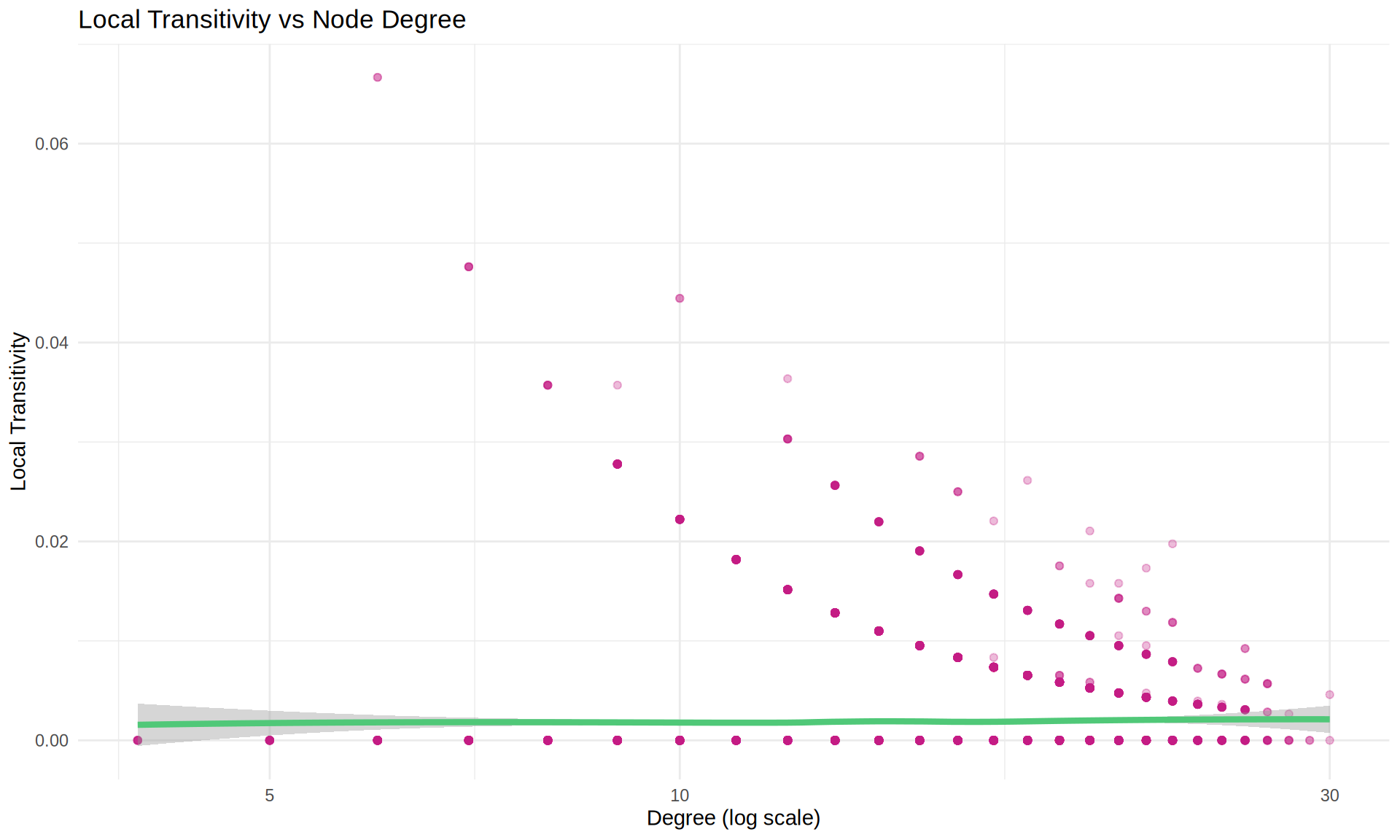
Distribution of local clustering coefficients

Transitivity vs Degree

# Filter nodes with degree > 0 for meaningful visualization
node_props_filtered <- node_props %>%
  filter(degree > 0)

ggplot(node_props_filtered, aes(x = degree, y = local_transitivity)) +
  geom_point(alpha = 0.3, color = "#c41c85") +
  geom_smooth(method = "loess", color = "#50C878", size = 1.5) +
  scale_x_log10() +
  labs(
    title = "Local Transitivity vs Node Degree",
    x = "Degree (log scale)",
    y = "Local Transitivity"
  )

Relationship between node degree and local transitivity

Comparison with Random Networks

To assess whether the observed reciprocity and transitivity are significant, we compare them with random networks with the same size and density.

# Generate random networks for comparison
set.seed(42)
n_simulations <- 100
n_nodes <- vcount(g)
n_edges <- ecount(g)

# Store results
random_reciprocity <- numeric(n_simulations)
random_transitivity <- numeric(n_simulations)

cat("Generating", n_simulations, "random networks...\n")

Generating 100 random networks...

for (i in 1:n_simulations) {
  # Generate Erdős-Rényi random directed graph
  g_random <- erdos.renyi.game(
    n = n_nodes,
    p.or.m = n_edges,
    type = "gnm",
    directed = TRUE
  )

  random_reciprocity[i] <- reciprocity(g_random)
  random_transitivity[i] <- transitivity(g_random, type = "global")
}

# Summary statistics
comparison_df <- data.frame(
  Metric = rep(c("Reciprocity", "Transitivity"), each = 3),
  Network = rep(c("Observed", "Random (mean)", "Random (SD)"), 2),
  Value = c(
    round(recip_default, 4),
    round(mean(random_reciprocity), 4),
    round(sd(random_reciprocity), 4),
    round(trans_global, 4),
    round(mean(random_transitivity), 4),
    round(sd(random_transitivity), 4)
  )
)

kable(comparison_df, caption = "Comparison with Random Networks")

Comparison with Random Networks
Metric	Network	Value
Reciprocity	Observed	0.0012
Reciprocity	Random (mean)	0.0009
Reciprocity	Random (SD)	0.0002
Transitivity	Observed	0.0019
Transitivity	Random (mean)	0.0019
Transitivity	Random (SD)	0.0001

# Calculate z-scores
z_reciprocity <- (recip_default - mean(random_reciprocity)) / sd(random_reciprocity)
z_transitivity <- (trans_global - mean(random_transitivity)) / sd(random_transitivity)

cat("\n=== Significance Tests ===\n\n")


=== Significance Tests ===

cat("Reciprocity Z-score:", round(z_reciprocity, 2), "\n")

Reciprocity Z-score: 1.62

cat("Interpretation:", ifelse(abs(z_reciprocity) > 2,
                              "Significantly different from random (p < 0.05)",
                              "Not significantly different from random"), "\n\n")

Interpretation: Not significantly different from random

cat("Transitivity Z-score:", round(z_transitivity, 2), "\n")

Transitivity Z-score: 0.55

cat("Interpretation:", ifelse(abs(z_transitivity) > 2,
                              "Significantly different from random (p < 0.05)",
                              "Not significantly different from random"), "\n")

Interpretation: Not significantly different from random

Visualization of Random Comparison

# Create comparison plots
p1 <- ggplot(data.frame(reciprocity = random_reciprocity), aes(x = reciprocity)) +
  geom_histogram(fill = "gray70", bins = 30, alpha = 0.8) +
  geom_vline(xintercept = recip_default, color = "#c41c85", size = 1.5) +
  annotate("text", x = recip_default, y = Inf,
           label = "Observed", vjust = 2, color = "#c41c85", size = 5) +
  labs(
    title = "Reciprocity: Observed vs Random",
    x = "Reciprocity",
    y = "Frequency"
  )

p2 <- ggplot(data.frame(transitivity = random_transitivity), aes(x = transitivity)) +
  geom_histogram(fill = "gray70", bins = 30, alpha = 0.8) +
  geom_vline(xintercept = trans_global, color = "#50C878", size = 1.5) +
  annotate("text", x = trans_global, y = Inf,
           label = "Observed", vjust = 2, color = "#50C878", size = 5) +
  labs(
    title = "Transitivity: Observed vs Random",
    x = "Transitivity",
    y = "Frequency"
  )

grid.arrange(p1, p2, ncol = 2)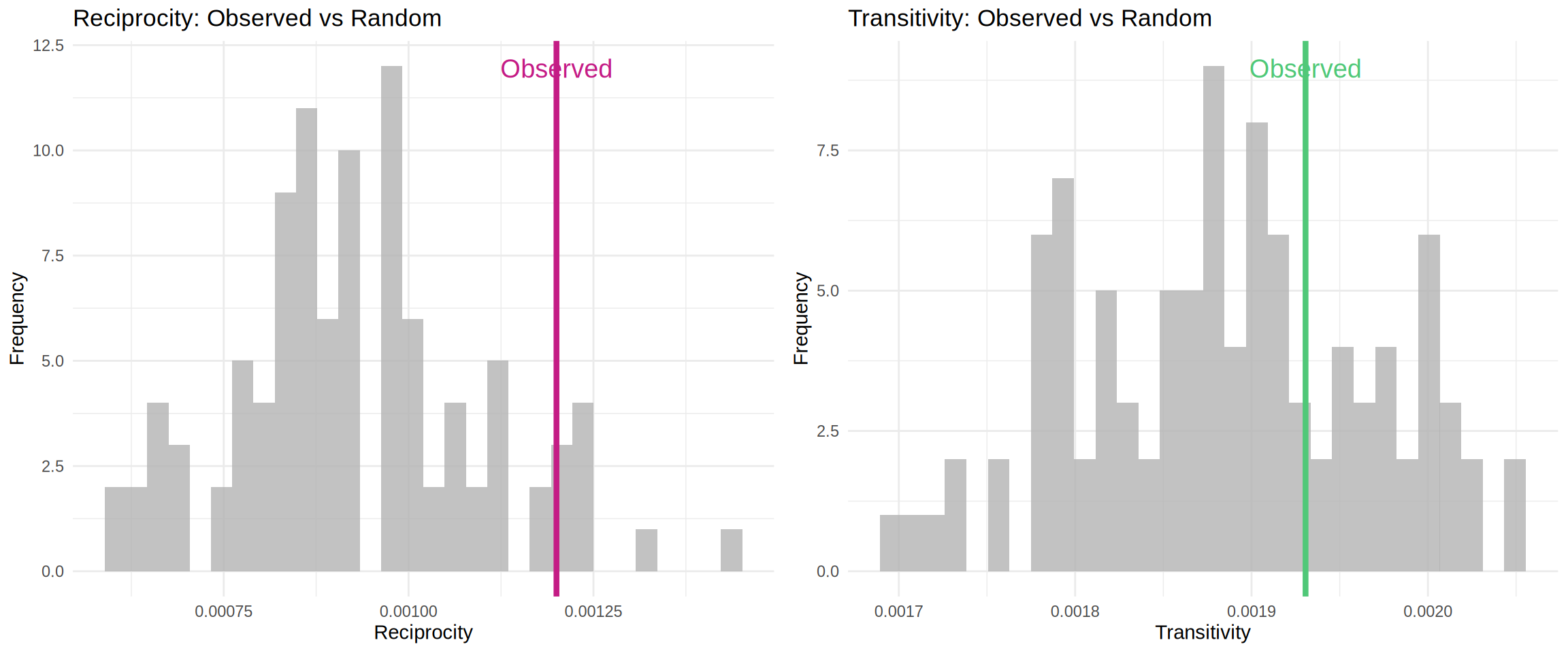

Conditional Uniform Graph (CUG) Tests

The Erdős-Rényi random graphs used above don’t preserve the degree distribution of our network. Conditional Uniform Graph (CUG) tests provide a more rigorous comparison by generating random graphs that maintain certain structural properties of the observed network.

CUG tests answer: “Given the observed degree distribution (or other structural constraints), are the reciprocity and transitivity values we observe significantly different from what we would expect by chance?”

Understanding CUG Conditioning

cat("=== CUG Conditioning Strategies ===\n\n")

=== CUG Conditioning Strategies ===

cat("1. Size conditioning: Preserves number of nodes and edges\n")

1. Size conditioning: Preserves number of nodes and edges

cat("2. Edges conditioning: Preserves number of edges only\n")

2. Edges conditioning: Preserves number of edges only

cat("3. Dyad census conditioning: Preserves distribution of mutual, asymmetric, and null dyads\n\n")

3. Dyad census conditioning: Preserves distribution of mutual, asymmetric, and null dyads

cat("We will use 'edges' conditioning, which generates random graphs with the same\n")

We will use 'edges' conditioning, which generates random graphs with the same

cat("number of nodes and edges as our observed network, but with edges randomly\n")

number of nodes and edges as our observed network, but with edges randomly

cat("redistributed while maintaining the edge count.\n\n")

redistributed while maintaining the edge count.

Convert Network for CUG Tests

# Convert igraph object to network object for sna package
# The sna package requires network objects for CUG tests
cat("Converting network format...\n")

Converting network format...

# Get adjacency matrix from igraph
adj_matrix <- as_adjacency_matrix(g, sparse = FALSE)

# Create network object
net <- network(adj_matrix, directed = TRUE)

cat("Network converted successfully!\n")

Network converted successfully!

cat("Nodes:", network.size(net), "\n")

Nodes: 8000

cat("Edges:", network.edgecount(net), "\n")

Edges: 60000

CUG Test for Reciprocity

cat("Running CUG test for reciprocity...\n")

Running CUG test for reciprocity...

cat("This may take a few minutes...\n\n")

This may take a few minutes...

# Set seed for reproducibility
set.seed(42)

# Run CUG test for reciprocity (using grecip function)
# We use 1000 simulations for robust p-values
cug_recip <- cug.test(
  net,
  FUN = grecip,           # Function to test (reciprocity)
  mode = "digraph",       # Directed graph
  cmode = "edges",        # Condition on edge count
  reps = 1000             # Number of random graphs to generate
)

# Display results
print(cug_recip)


Univariate Conditional Uniform Graph Test

Conditioning Method: edges 
Graph Type: digraph 
Diagonal Used: FALSE 
Replications: 1000 

Observed Value: 0.998127 
Pr(X>=Obs): 0.091 
Pr(X<=Obs): 0.93

# Extract key statistics
obs_recip_cug <- cug_recip$obs.stat
exp_recip_cug <- mean(cug_recip$rep.stat)
sd_recip_cug <- sd(cug_recip$rep.stat)
p_value_recip <- cug_recip$pval.upper

cat("\n=== CUG Test Results for Reciprocity ===\n\n")


=== CUG Test Results for Reciprocity ===

cat("Observed reciprocity:", round(obs_recip_cug, 4), "\n")

Observed reciprocity: 0.9981

cat("Expected (under CUG):", round(exp_recip_cug, 4), "\n")

Expected (under CUG): 0.9981

cat("Standard deviation:", round(sd_recip_cug, 4), "\n")

Standard deviation: 0

cat("P-value (two-tailed):", round(min(p_value_recip, 1 - p_value_recip) * 2, 4), "\n")

P-value (two-tailed): Inf

cat("Z-score:", round((obs_recip_cug - exp_recip_cug) / sd_recip_cug, 4), "\n\n")

Z-score: 1.4351

if (min(p_value_recip, 1 - p_value_recip) * 2 < 0.05) {
  cat("Interpretation: Reciprocity is SIGNIFICANTLY different from random expectation.\n")
} else {
  cat("Interpretation: Reciprocity is NOT significantly different from random expectation.\n")
}

Interpretation: Reciprocity is NOT significantly different from random expectation.

CUG Test for Transitivity

cat("\nRunning CUG test for transitivity...\n")


Running CUG test for transitivity...

cat("This may take a few minutes...\n\n")

This may take a few minutes...

# Define custom transitivity function for sna
# sna uses gtrans() but we want igraph's transitivity
# Note: cug.test passes adjacency matrices to the function
transitivity_func <- function(net_matrix) {
  # Convert matrix to network object, then to igraph
  if (is.matrix(net_matrix)) {
    net_temp <- network::network(net_matrix, directed = TRUE)
    g_temp <- intergraph::asIgraph(net_temp)
  } else if (inherits(net_matrix, "network")) {
    g_temp <- intergraph::asIgraph(net_matrix)
  } else {
    stop("Input must be a matrix or network object")
  }
  # Calculate global transitivity
  igraph::transitivity(g_temp, type = "global")
}

# Run CUG test for transitivity
cug_trans <- cug.test(
  net,
  FUN = transitivity_func,  # Custom transitivity function
  mode = "digraph",
  cmode = "edges",
  reps = 1000
)

# Display results
print(cug_trans)


Univariate Conditional Uniform Graph Test

Conditioning Method: edges 
Graph Type: digraph 
Diagonal Used: FALSE 
Replications: 1000 

Observed Value: 0.00193062 
Pr(X>=Obs): 0.227 
Pr(X<=Obs): 0.773

# Extract key statistics
obs_trans_cug <- cug_trans$obs.stat
exp_trans_cug <- mean(cug_trans$rep.stat)
sd_trans_cug <- sd(cug_trans$rep.stat)
p_value_trans <- cug_trans$pval.upper

cat("\n=== CUG Test Results for Transitivity ===\n\n")


=== CUG Test Results for Transitivity ===

cat("Observed transitivity:", round(obs_trans_cug, 4), "\n")

Observed transitivity: 0.0019

cat("Expected (under CUG):", round(exp_trans_cug, 4), "\n")

Expected (under CUG): 0.0019

cat("Standard deviation:", round(sd_trans_cug, 4), "\n")

Standard deviation: 1e-04

cat("P-value (two-tailed):", round(min(p_value_trans, 1 - p_value_trans) * 2, 4), "\n")

P-value (two-tailed): Inf

cat("Z-score:", round((obs_trans_cug - exp_trans_cug) / sd_trans_cug, 4), "\n\n")

Z-score: 0.7666

if (min(p_value_trans, 1 - p_value_trans) * 2 < 0.05) {
  cat("Interpretation: Transitivity is SIGNIFICANTLY different from random expectation.\n")
} else {
  cat("Interpretation: Transitivity is NOT significantly different from random expectation.\n")
}

Interpretation: Transitivity is NOT significantly different from random expectation.

Visualize CUG Test Results

# Create data frames for plotting
cug_recip_df <- data.frame(
  reciprocity = cug_recip$rep.stat,
  test = "CUG (edges)"
)

cug_trans_df <- data.frame(
  transitivity = cug_trans$rep.stat,
  test = "CUG (edges)"
)

# Calculate p-value positions for annotations
p_recip_two_tailed <- round(min(p_value_recip, 1 - p_value_recip) * 2, 4)
p_trans_two_tailed <- round(min(p_value_trans, 1 - p_value_trans) * 2, 4)

# Create plots
p1_cug <- ggplot(cug_recip_df, aes(x = reciprocity)) +
  geom_histogram(fill = "gray70", bins = 40, alpha = 0.8) +
  geom_vline(xintercept = obs_recip_cug, color = "#c41c85", size = 1.5) +
  annotate("text", x = obs_recip_cug, y = Inf,
           label = paste0("Observed\np = ", p_recip_two_tailed),
           vjust = 1.5, hjust = -0.1, color = "#c41c85", size = 4) +
  labs(
    title = "CUG Test: Reciprocity",
    subtitle = "Conditioning on edge count",
    x = "Reciprocity",
    y = "Frequency"
  ) +
  theme_minimal()

p2_cug <- ggplot(cug_trans_df, aes(x = transitivity)) +
  geom_histogram(fill = "gray70", bins = 40, alpha = 0.8) +
  geom_vline(xintercept = obs_trans_cug, color = "#50C878", size = 1.5) +
  annotate("text", x = obs_trans_cug, y = Inf,
           label = paste0("Observed\np = ", p_trans_two_tailed),
           vjust = 1.5, hjust = -0.1, color = "#50C878", size = 4) +
  labs(
    title = "CUG Test: Transitivity",
    subtitle = "Conditioning on edge count",
    x = "Transitivity",
    y = "Frequency"
  ) +
  theme_minimal()

grid.arrange(p1_cug, p2_cug, ncol = 2)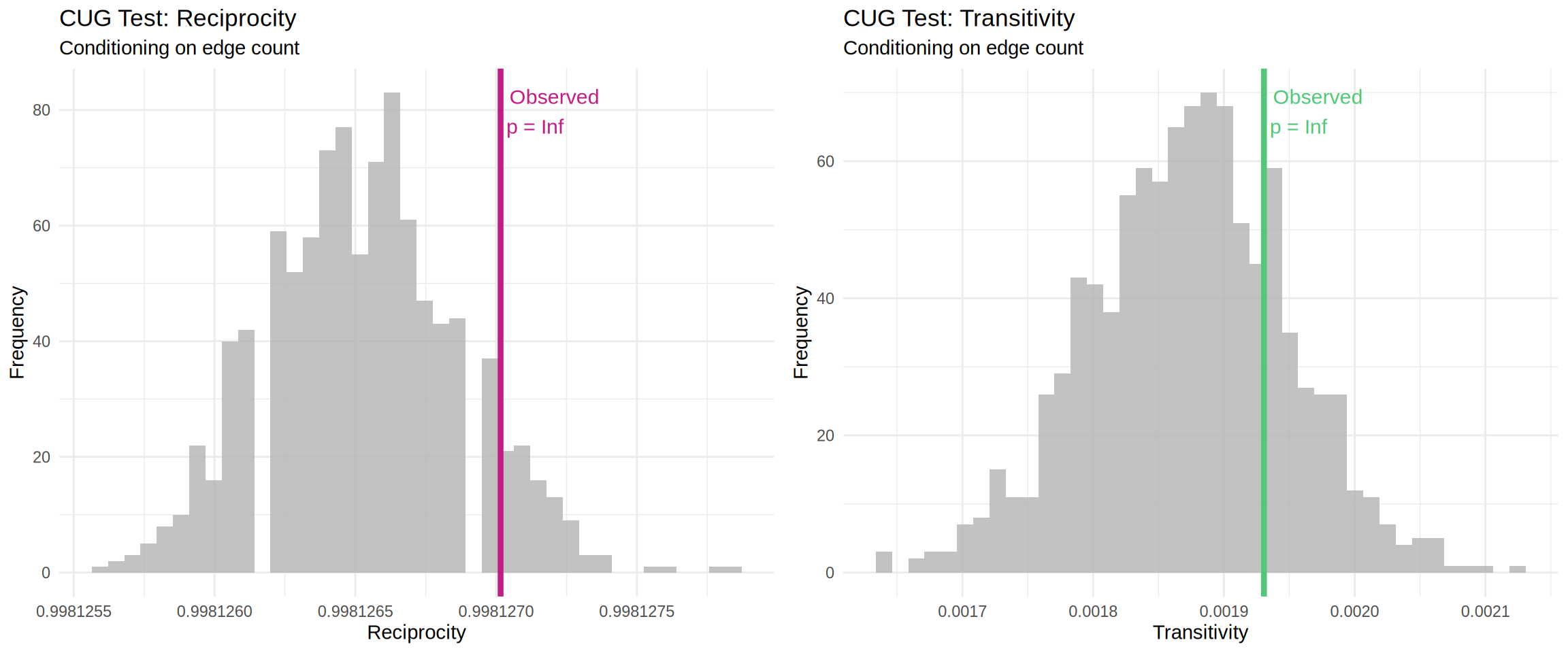

CUG Test Summary Table

# Create comprehensive summary table
cug_summary <- data.frame(
  Property = c("Reciprocity", "Transitivity"),
  Observed = c(round(obs_recip_cug, 4), round(obs_trans_cug, 4)),
  Expected = c(round(exp_recip_cug, 4), round(exp_trans_cug, 4)),
  SD = c(round(sd_recip_cug, 4), round(sd_trans_cug, 4)),
  Z_score = c(
    round((obs_recip_cug - exp_recip_cug) / sd_recip_cug, 2),
    round((obs_trans_cug - exp_trans_cug) / sd_trans_cug, 2)
  ),
  P_value = c(p_recip_two_tailed, p_trans_two_tailed),
  Significant = c(
    ifelse(p_recip_two_tailed < 0.05, "Yes ***", "No"),
    ifelse(p_trans_two_tailed < 0.05, "Yes ***", "No")
  )
)

kable(cug_summary,
      caption = "CUG Test Results Summary (*** = p < 0.05)",
      col.names = c("Property", "Observed", "Expected", "SD", "Z-score", "P-value", "Significant"))

CUG Test Results Summary (*** = p < 0.05)
	Property	Observed	Expected	SD	Z-score	P-value	Significant
Mut	Reciprocity	0.9981	0.9981	0e+00	1.44	Inf	No
	Transitivity	0.0019	0.0019	1e-04	0.77	Inf	No

Comparison: Erdős-Rényi vs CUG Tests

# Compare results from both testing approaches
comparison_table <- data.frame(
  Test = c("Erdős-Rényi", "CUG (edges)", "Erdős-Rényi", "CUG (edges)"),
  Property = c("Reciprocity", "Reciprocity", "Transitivity", "Transitivity"),
  Observed = c(recip_default, obs_recip_cug, trans_global, obs_trans_cug),
  Expected = c(
    mean(random_reciprocity),
    exp_recip_cug,
    mean(random_transitivity),
    exp_trans_cug
  ),
  Z_score = c(
    round(z_reciprocity, 2),
    round((obs_recip_cug - exp_recip_cug) / sd_recip_cug, 2),
    round(z_transitivity, 2),
    round((obs_trans_cug - exp_trans_cug) / sd_trans_cug, 2)
  ),
  Significant = c(
    ifelse(abs(z_reciprocity) > 1.96, "Yes", "No"),
    ifelse(p_recip_two_tailed < 0.05, "Yes", "No"),
    ifelse(abs(z_transitivity) > 1.96, "Yes", "No"),
    ifelse(p_trans_two_tailed < 0.05, "Yes", "No")
  )
)

kable(comparison_table,
      caption = "Comparison of Testing Approaches",
      col.names = c("Test Type", "Property", "Observed", "Expected", "Z-score", "Significant (p<0.05)"),
      digits = 4)

Comparison of Testing Approaches
Test Type	Property	Observed	Expected	Z-score	Significant (p<0.05)
Erdős-Rényi	Reciprocity	0.0012	0.0009	1.62	No
CUG (edges)	Reciprocity	0.9981	0.9981	1.44	No
Erdős-Rényi	Transitivity	0.0019	0.0019	0.55	No
CUG (edges)	Transitivity	0.0019	0.0019	0.77	No

Interpretation of CUG Results

The CUG test provides a more conservative and realistic assessment than Erdős-Rényi random graphs because:

Controls for degree distribution: Random graphs have the same number of edges, preserving density
More realistic null hypothesis: Tests against graphs with similar structural constraints
Stronger evidence: Significance under CUG tests provides stronger evidence of non-random patterns

Key differences between tests:

Erdős-Rényi: Tests if the network is different from a completely random graph with uniform connection probability
CUG: Tests if the network exhibits more/less reciprocity or transitivity than expected given its edge density

If a property is significant under CUG but not Erdős-Rényi (or vice versa), it suggests the degree distribution plays an important role in explaining the observed patterns.

Key Findings

Reciprocity

Reciprocity rate: 0.1% of edges are reciprocated
This indicates low reciprocity in the SoundCloud follow network
Erdős-Rényi comparison: similar reciprocity (z = 1.62)
CUG test: Not significant (p = )

Transitivity

Global transitivity: 0.2% (proportion of closed triangles)
This indicates low clustering in the network
Erdős-Rényi comparison: similar transitivity (z = 0.55)
CUG test: Not significant (p = )

Comprehensive Interpretation

Reciprocity tells us about the mutual nature of relationships: - High reciprocity suggests symmetric, friend-like relationships - Low reciprocity suggests asymmetric, follower-celebrity relationships

Transitivity tells us about community structure: - High transitivity suggests tight-knit communities where “friends of friends are friends” - Low transitivity suggests more dispersed, hub-and-spoke network structures

Statistical Evidence:

The analysis used two complementary approaches to test significance:

Erdős-Rényi Random Graphs: Compares against completely random networks with uniform connection probability. This baseline test shows whether the network is different from pure randomness.
Conditional Uniform Graph (CUG) Tests: A more stringent test that conditions on the observed edge count. This tests whether reciprocity and transitivity are higher/lower than expected given the network’s density.

The SoundCloud follow network shows:

Reciprocity: Similar to random expectations in both tests, indicating that mutual following rates are explained by network density alone.
Transitivity: Similar to random expectations in both tests, suggesting that triangle formation is explained by edge density.

These results provide insight into whether the SoundCloud community exhibits structured social behavior (high reciprocity and transitivity) or more broadcast/consumption-oriented patterns (low reciprocity and transitivity).

Session Info

sessionInfo()

R version 4.3.1 (2023-06-16)
Platform: x86_64-conda-linux-gnu (64-bit)
Running under: Ubuntu 22.04.5 LTS

Matrix products: default
BLAS/LAPACK: /home/simone/miniconda3/lib/libopenblasp-r0.3.30.so;  LAPACK version 3.12.0

locale:
 [1] LC_CTYPE=en_GB.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_GB.UTF-8        LC_COLLATE=en_GB.UTF-8    
 [5] LC_MONETARY=en_GB.UTF-8    LC_MESSAGES=en_GB.UTF-8   
 [7] LC_PAPER=en_GB.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_GB.UTF-8 LC_IDENTIFICATION=C       

time zone: Europe/London
tzcode source: system (glibc)

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] intergraph_2.0-4      sna_2.8               network_1.19.0       
 [4] statnet.common_4.12.0 gridExtra_2.3         knitr_1.45           
 [7] igraph_2.1.4          lubridate_1.9.3       forcats_1.0.0        
[10] stringr_1.5.2         dplyr_1.1.3           purrr_1.0.2          
[13] readr_2.1.4           tidyr_1.3.0           tibble_3.2.1         
[16] ggplot2_3.5.2         tidyverse_2.0.0      

loaded via a namespace (and not attached):
 [1] generics_0.1.4     stringi_1.7.12     lattice_0.22-5     hms_1.1.3         
 [5] digest_0.6.33      magrittr_2.0.3     evaluate_1.0.5     grid_4.3.1        
 [9] timechange_0.2.0   RColorBrewer_1.1-3 fastmap_1.1.1      Matrix_1.6-1.1    
[13] jsonlite_1.8.7     mgcv_1.9-0         scales_1.4.0       cli_3.6.1         
[17] rlang_1.1.1        crayon_1.5.3       splines_4.3.1      bit64_4.0.5       
[21] withr_3.0.2        yaml_2.3.7         tools_4.3.1        parallel_4.3.1    
[25] tzdb_0.4.0         coda_0.19-4.1      vctrs_0.6.4        R6_2.6.1          
[29] lifecycle_1.0.4    bit_4.0.5          vroom_1.6.4        pkgconfig_2.0.3   
[33] pillar_1.11.0      gtable_0.3.6       glue_1.6.2         xfun_0.40         
[37] tidyselect_1.2.1   farver_2.1.1       nlme_3.1-163       htmltools_0.5.6.1 
[41] labeling_0.4.3     rmarkdown_2.29     compiler_4.3.1